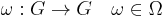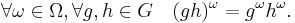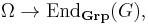Group with operators

In abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.

Groups with operators were extensively studied by Emmy Noether and her school in the 1920s. She employed the concept in her original formulation of the three Noether isomorphism theorems.

1 Definition
2 Category-theoretic remarks
3 Examples
4 Applications
5 See also
6 References

Definition

A group with operators (G, $\Omega$ ) is a group G together with a family of functions $\Omega$ :

$\omega�: G \to G \quad \omega \in \Omega$

which are distributive with respect to the group operation. $\Omega$ is called the operator domain, and its elements are called the homotheties of G.

We denote the image of a group element g under a function $\omega$ with $g^\omega$ . The distributivity can then be expressed as

$\forall \omega \in \Omega, \forall g,h \in G \quad (gh)^{\omega} = g^{\omega}h^{\omega} .$

A subgroup S of G is called a stable subgroup, $\omega$ -subgroup or $\Omega$ -invariant subgroup if it respects the homotheties, that is

$\forall s \in S, \forall \omega \in \Omega�: s^\omega \in S.$

Category-theoretic remarks

In category theory, a group with operators can be defined as an object of a functor category Grp^M where M is a monoid (i.e., a category with one object) and Grp denotes the category of groups. This definition is equivalent to the previous one.

A group with operators is also a mapping

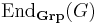$\Omega\rightarrow\operatorname{End}_{\mathbf{Grp}}(G),$

where $\operatorname{End}_{\mathbf{Grp}}(G)$ is the set of group endomorphisms of G.

Examples

Given any group G, (G, ∅) is trivially a group with operators
Given an R-module M, the group M operates on the operator domain R by scalar multiplication. More concretely, every vector space is a group with operators.

Applications

The Jordan–Hölder theorem also holds in the context of operator groups. The requirement that a group have a composition series is analogous to that of compactness in topology, and can sometimes be too strong a requirement. It is natural to talk about "compactness relative to a set", i.e. talk about composition series where each (normal) subgroup is an operator-subgroup relative to the operator set X, of the group in question.

References

Bourbaki, Nicolas (1998). Elements of Mathematics : Algebra I Chapters 1-3. Springer-Verlag. ISBN 3-540-64243-9.